Netscape Preferred . . . . . . . . . . . . . . . . . . . . . . . . e-mail [email protected]
This is an Experimental Teaching Page
Aimed at Chaos and the World Wide Web
Fractals, if they point to aspects of God point to the human fascination with pattern. The endurance of patterns may well point to an organic harmony or resonance - the stability of forms is deeply appealing though finally distracting. To mediate order is to promote peace - to mediate order is to be human. To go further and abstract a deity is to forego vision - what we see is what we see and that is wonder.Keith Russell Quoted in Brennan, Paul (1997) "God Cauliflowers Mandelbrot", Philosopher No5, p.30










CHAOS
Images from James Gleick's
CHAOS The Software
Assembled by Keith Russell

Chaos: Play the Triangle Game
1) Draw a triangle.2) Name the corners 1,2 - 3,4 - 5,6.
3) Prick and mark a point at random inside the area of the triangle.
4) Throw a die and then using the number (1-6),
draw another point half way between the first point
and the corner selected by the throw of the die.
(Note: do not draw a line connecting the points.)
5) Throw the die again and repeat the process.
6) The result, after many iterations, will look something
like the image above.

Part of the most famous Chaos image of all: the Mandelbrot set, named after its discoverer, Benoit Mandelbrot.. This image holds a deep fascination as it can be enlarged over and over with the same patterns emerging. (See Gleick, pp.221-226)



The Koch Snowflake. "A rough but vigorous model of a coastline," in Mandelbrotís words. To construct a Koch curve, begin with a triangle with sides of length 1. At the middle of each side, add a new triangle one-third the size; and so on. The length of the boundary is 3 x 4/3 x 4/3 x 4/3 . . . infinity. Yet the area remains less than the area of a circle drawn around the original triangle. Thus an infinitely long line surrounds a finite area. (Gleick, p.99)

The Cantor Dust. Begin with a line; remove the middle third; then remove the middle third of the remaining segments; and so on. The Cantor set is the dust of the points that remain. They are infinitely many, but their total length is 0. (Gleick, p.93)
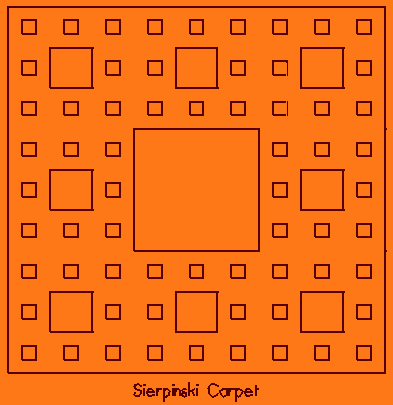
Constructing With Holes. A few mathematicians in the early twentieth century conceived monstrous-seeming objects made by the techniques of adding or removing infinitely many parts. One such shape is the Sierpinski carpet, constructed by cutting the centre one-ninth of a square; then cutting out the centre of the eight smaller squares that remain; and so on. (Gleick, p.101)
References:
Gleick, James. 1987, Chaos: Making a New Science, NY: Viking. 1990, Chaos: The Software, Sausalito, CA: Autodesk.
HOT LINKS
Chaos in the Classroom - by Robert Devaney
Fractal images created by Art Baker
OTHER THINGS
ABC TV
I*EARN AUSTRALIA
Youth Making a Difference throughTelecommunications
See 3D models by 4-5 year-olds
See a selection of work by the author



